控江中学高中三年级月考数学卷
1、 填空题
1. 函数
的概念域为__________
2. 已知
，且
、
（
是虚数单位）是实系数一元二次方程
的两个根，那样
的值为__________
3. 
除以
的余数是__________
4. 函数
的反函数
__________
5. 在无穷等比数列
中，
，
，则__________
6. 设
、
分别为双曲线
的左、右焦点，若在双曲线右支上存
在点
，满足
，则该双曲线的渐近线方程为__________
7. 在等差数列中，
，则
的最小值为__________
8. 函数
图像向左平移
单位后为奇函数，则
的最小正值为__________
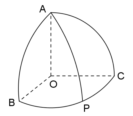
9. 如图，
是球面上三点，且
两两垂直，若是球的大圆所在弧
的中点，则直线
与
所成角的大小为__________
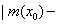
10. 函数的零点个数为__________
11. 如图，在△
中，，
，在斜边上，且
，则
的值为__________
12. 已知函数
，关于
的不等式
在区间上有解，
则实数
的取值范围为__________
13. 已知，
的最小值为__________
14. 设
、
、是集合，称为有序三元组，假如集合、、满足
，且，则称有序三元组为最小相交（其中
表示集合
中的元素个数），如集合
，，
就是最小相交有
序三元组，则由集合的子集构成的最小相交有序三元组的个数是__________
2、 选择题
15. 全集为，集合
，
，则集合
可表示为（ ）
A. B. 
C. 
D. 
16. 某单位有840名职工，现使用系统抽样办法，抽取42人做问卷调查，将840人按1、2、
…、840随机编号，则抽取的42人中，编号落入区间的人数为（ ）
A. 11 B. 12 C. 13 D. 14
17. 等差数列的前项和为
，若
，则下列结论：①，②，
③，④，其中正确的结论有（ ）个
A. 1 B. 2 C. 3 D. 4
18. 已知向量序列：、
、、…、、… 满足如下条件：，，
且
，则
、
、、…、
、… 中的最
小项是（ ）
A. 
B. C. D. 没有
3、 解答卷
19. 在△中，角所对的边分别为
，满足
；
（1）求角；
（2）求的取值范围；
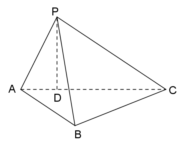
20. 如图，三棱锥
，平面，且垂足在棱
上，，
，，；
（1）证明△
为直角三角形；
（2）求点到平面的距离；
21. 曲线上动点到定点与定直线的距离之比为常数；
（1）求曲线的轨迹方程；
（2）设圆心为
的圆 
与曲线交于点与点
，求
的最小值，并求此时圆的方程；
22. 若数列的每一项都不等于零，且对于任意的
，都有（为常数），
则称数列为“类等比数列”；已知数列满足：，对于任意的，
都有；
（1）求证：数列是“类等比数列”；
（2）若是单调递减数列，求实数的取值范围；
（3）若，求数列的前项之积取最大值时的值；
23. 已知函数在区间上的最大值为，最小值为，
记；
（1）求实数、的值；
（2）若不等式对任意恒成立，求实数的范围；
（3）对于概念在
上的函数，设
，，用任意的
将划分为个小区间，其中，若存在一个常数，使得
恒成立，则称函数为上
的有界变差函数；
① 试证明函数是在上的有界变差函数，并求出的最小值；
② 写出是在上的有界变差函数的一个充分条件，使上述结论成为其特例；
（不需要证明）
参考答案
1、 填空题
1. 2. 1 3. 3 4. 
5.
6. 7. 48 8. 9. 10. 2 11. 6
12. 13. 8 14. 7680
2、 选择题
15. C 16. B 17. B 18. C
3、 解答卷
19.（1）；（2）； 20.（1）略；（2）；
21.（1）；（2）最小值，；
22.（1）略；（2）；（3）；
23.（1），；（2）；（3）
；
